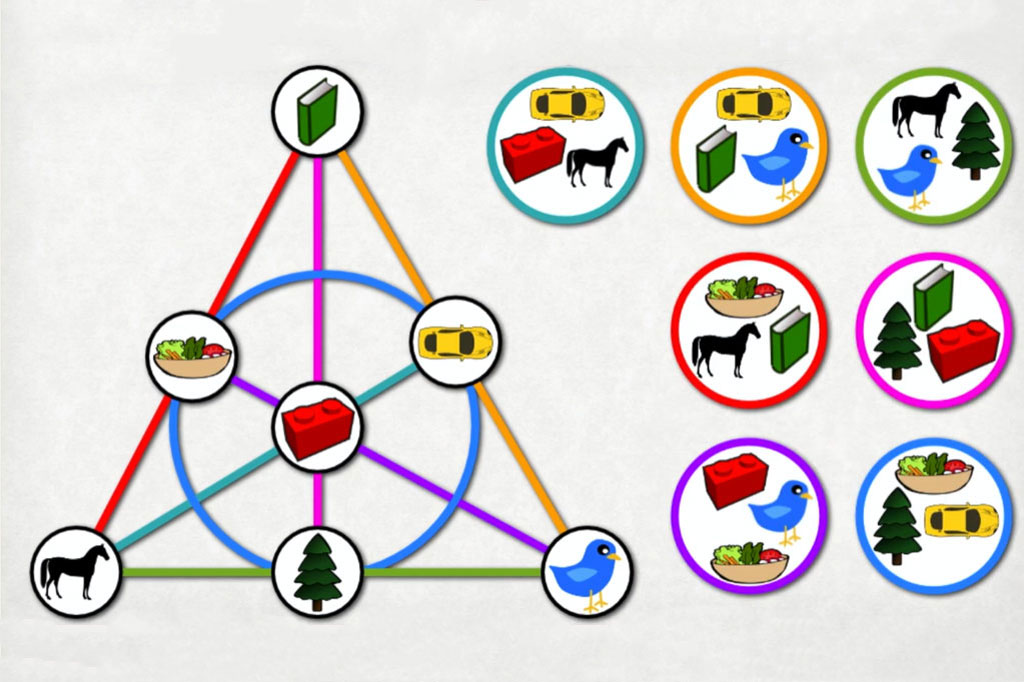
Se já jogou Spot It! (também conhecido como Dobble), provavelmente já se perguntou o mesmo que milhões de jogadores:
Como é que todos os pares de cartas têm exatamente UM símbolo em comum?
Parece magia… mas, na verdade, é matemática, especificamente, planos projetivos finitos, combinatória e aritmética modular.
Table of Contents
1. O conceito matemático central: planos projetivos finitos
Um baralho padrão do Spot It! baseia-se na estrutura de um plano projetivo finito de ordem n.
Um plano projetivo de ordem n tem estas propriedades:
- Cada carta tem (n + 1) símbolos.
- Há (n² + n + 1) símbolos no total.
- Há (n² + n + 1) cartas no total.
- Quaisquer duas cartas partilham exatamente UM símbolo.
- Quaisquer dois símbolos aparecem juntos em exatamente UMA carta.
Para o Spot It!, a ordem utilizada é:
- n = 7
O que dá:
- Símbolos por carta: n + 1 = 8
- Cartas no baralho: n² + n + 1 = 57
- Símbolos únicos: 57
Isto explica porque é que os baralhos Spot It! têm normalmente 55 cartas (duas são removidas para caber na caixa do produto).
2. Por que apenas um símbolo correspondente funciona
Matematicamente, se cada par de cartas deve ter exatamente um símbolo em comum (nem mais, nem menos), a estrutura deve impedir:
- zero correspondências (sublap)
- múltiplas correspondências (overlap)
O design de um plano projetivo garante isso:
- Cada símbolo aparece em n + 1 cartas.
- Cada carta tem n + 1 símbolos.
- A distribuição dos símbolos é equilibrada através de construções aritméticas modulares.
3. Como as cartas são realmente geradas
Aqui está o método construtivo simplificado usado para construir um baralho quando n é primo (como 7).
Passo A: Crie a carta “infinita”
Símbolos:
- ∞, a0, a1, a2, a3, a4, a5, a6 (8 símbolos no total)
Passo B: Crie n grupos de n cartas
Para cada linha r (0–6) e cada coluna c (0–6), crie uma carta:
- símbolo: a_r
- mais os símbolos b_{(r×1+c)}, b_{(r×2+c)}, …, b_{(r×7+c)} (todos módulo 7)
Isso garante que os alinhamentos dos padrões sempre se sobreponham uma e apenas uma vez.
Passo C: Adicione as n + 1 cartas finais de «inclinação»
Elas garantem que as relações diagonais correspondam conforme exigido pelo plano projetivo.
Quando montado, o baralho forma uma estrutura matemática perfeita, na qual:
- Cada carta cruza todas as outras cartas em exatamente um símbolo.
4. Por que os números primos são importantes
Esta construção funciona perfeitamente quando n é um número primo (2, 3, 5, 7, 11, …) ou uma potência prima.
É por isso que o Spot It! usa:
- n = 7 (um primo)
- Cartas = 57 (máximo possível para esta ordem)
Se tentar construir o seu próprio baralho com:
- n = 6
- n = 10
- n = 12
Rapidamente descobrirá que é impossível satisfazer a regra de «apenas uma correspondência», porque os planos projetivos não existem para a maioria das ordens que não são potências primárias.
5. Por que o baralho tem 55 cartas, e não 57
Em teoria, um plano projetivo n = 7 perfeito resulta em 57 cartas.
Mas os baralhos Spot It! geralmente vêm com:
- 55 cartas (padrão)
- 31 cartas (versão júnior)
- Contagens temáticas personalizadas
Os fabricantes reduzem o baralho para:
- Consistência do tamanho da caixa
- Custo de fabricação
- Conjuntos temáticos
- Opções de design de expansão
Mesmo com cartas removidas, a estrutura de correspondência ainda parece “mágica” para os jogadores.
6. A bela simetria do sistema

Um plano projetivo totalmente realizado tem um equilíbrio incrível:
- Cada símbolo aparece o mesmo número de vezes.
- Todas as cartas se comportam de forma idêntica.
- Todo o sistema é simétrico e «justo».
É essa simetria que dá ao Spot It! a sua jogabilidade suave, onde nenhuma carta é mais fácil ou mais difícil de combinar do que as outras.
7. Pode criar o seu próprio baralho Spot It!
Sim! Desde que siga:
- Escolha um número primo n.
- Use n² + n + 1 como o total de símbolos e cartas.
- Coloque n + 1 símbolos em cada carta.
- Construa usando aritmética modular ou um gerador de plano projetivo.
Por exemplo:
| n | Símbolos por carta | Total de cartas | Notas |
|---|---|---|---|
| 2 | 3 | 7 | Conjunto de demonstração pequeno |
| 3 | 4 | 13 | Opções temáticas pequenas |
| 5 | 6 | 31 | Tamanho personalizado popular |
| 7 | 8 | 57 | Tamanho clássico do Spot It! |
É por isso que as versões Print-and-Play (PnP) feitas por fãs costumam usar ordens primárias.