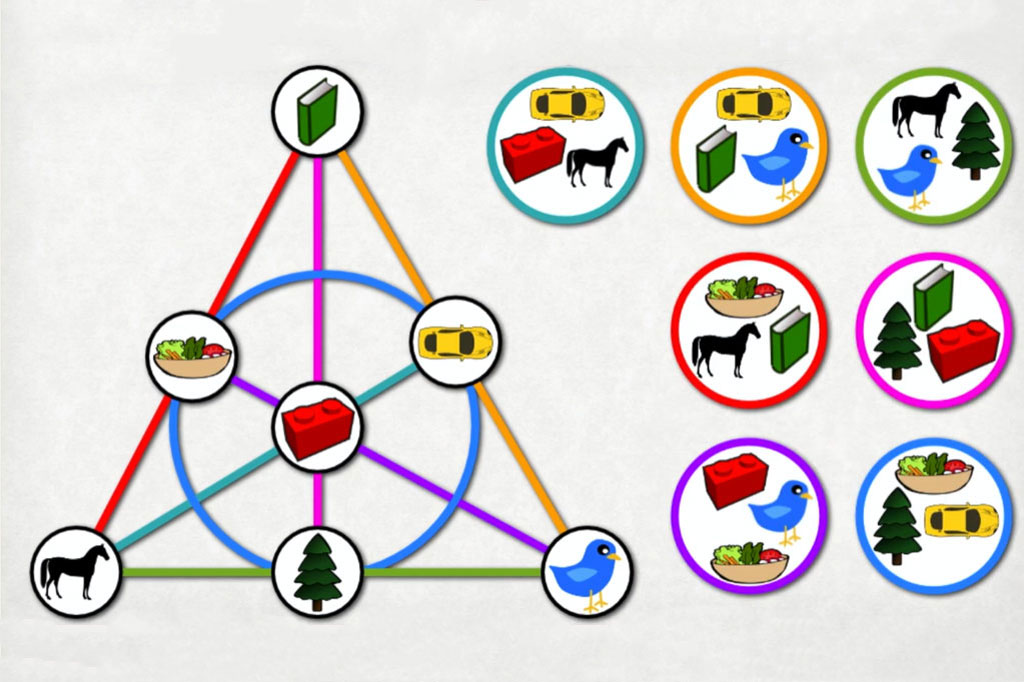
Wenn Sie schon einmal Spot It! (auch bekannt als Dobble) gespielt haben, haben Sie sich wahrscheinlich dieselbe Frage gestellt, über die schon Millionen von Spielern nachgedacht haben:
Wie um alles in der Welt kann jedes Kartenpaar genau EIN übereinstimmendes Symbol haben?
Es fühlt sich wie Zauberei an … aber eigentlich ist es Mathematik, genauer gesagt endliche projektive Ebenen, Kombinatorik und modulare Arithmetik.
Table of Contents
1. Das mathematische Kernkonzept: Endliche projektive Ebenen
Ein Standard-Spot It!-Kartenspiel basiert auf der Struktur einer endlichen projektiven Ebene der Ordnung n.
Eine projektive Ebene der Ordnung n hat folgende Eigenschaften:
- Jede Karte hat (n + 1) Symbole.
- Es gibt insgesamt (n² + n + 1) Symbole.
- Es gibt insgesamt (n² + n + 1) Karten.
- Zwei beliebige Karten haben genau EIN Symbol gemeinsam.
- Zwei beliebige Symbole erscheinen zusammen auf genau EINER Karte.
Für Spot It! wird folgende Ordnung verwendet:
- n = 7
Daraus ergibt sich:
- Symbole pro Karte: n + 1 = 8
- Karten im Kartenspiel: n² + n + 1 = 57
- Einzigartige Symbole: 57
Dies erklärt, warum Spot It!-Kartenspiele in der Regel 55 Karten enthalten (zwei werden entfernt, damit sie in die Verpackung passen).
2. Warum nur ein übereinstimmendes Symbol funktioniert
Mathematisch gesehen muss die Struktur Folgendes verhindern, wenn jedes Kartenpaar genau ein Symbol gemeinsam haben muss (nicht mehr und nicht weniger):
- keine Übereinstimmungen (Unterlappung)
- mehrere Übereinstimmungen (Überlappung)
Das Design einer projektiven Ebene garantiert dies:
- Jedes Symbol erscheint auf n + 1 Karten.
- Jede Karte hat n + 1 Symbole.
- Die Symbolverteilung wird durch modulare arithmetische Konstruktionen ausgeglichen.
3. Wie die Karten tatsächlich generiert werden
Hier ist die vereinfachte konstruktive Methode zum Erstellen eines Kartenspiels, wenn n eine Primzahl ist (z. B. 7).
Schritt A: Erstellen Sie die „unendliche” Karte
Symbole:
- ∞, a0, a1, a2, a3, a4, a5, a6 (insgesamt 8 Symbole)
Schritt B: Erstellen Sie n Gruppen mit jeweils n Karten
Erstellen Sie für jede Zeile r (0–6) und jede Spalte c (0–6) eine Karte:
- Symbol: a_r
- plus die Symbole b_{(r×1+c)}, b_{(r×2+c)}, …, b_{(r×7+c)} (alle modulo 7)
Dadurch wird sichergestellt, dass sich die Musterausrichtungen immer genau einmal überlappen.
Schritt C: Fügen Sie die letzten n + 1 „Neigungskarten” hinzu
Diese stellen sicher, dass die diagonalen Beziehungen den Anforderungen der projektiven Ebene entsprechen.
Wenn das Kartenspiel zusammengesetzt ist, bildet es eine perfekte mathematische Struktur, in der
- jede Karte jede andere Karte genau an einem Symbol schneidet.
4. Warum Primzahlen wichtig sind
Diese Konstruktion funktioniert einwandfrei, wenn n eine Primzahl (2, 3, 5, 7, 11, …) oder eine Primzahlpotenz ist.
Deshalb verwendet Spot It!
- n = 7 (eine Primzahl)
- Karten = 57 (maximal möglich für diese Reihenfolge)
Wenn Sie versuchen, Ihr eigenes Set mit folgenden Werten zu erstellen:
- n = 6
- n = 10
- n = 12
werden Sie schnell feststellen, dass es unmöglich ist, die Regel „nur eine Übereinstimmung” zu erfüllen, da es für die meisten Ordnungen, die keine Primzahlpotenzen sind, keine projektiven Ebenen gibt.
5. Warum das Kartenspiel 55 Karten hat und nicht 57
Theoretisch ergibt eine perfekte projektive Ebene mit n = 7 57 Karten.
Aber Spot It!-Kartenspiele werden normalerweise mit folgenden Karten geliefert:
- 55 Karten (Standard)
- 31 Karten (Junior-Version)
- Individuelle thematische Anzahlen
Die Hersteller reduzieren die Anzahl der Karten aus folgenden Gründen:
- Gleichbleibende Größe der Verpackung
- Herstellungskosten
- Thematische Sets
- Entscheidungen zum Design von Erweiterungen
Selbst mit entfernten Karten fühlt sich die Übereinstimmungsstruktur für die Spieler immer noch „magisch” an.
6. Die schöne Symmetrie des Systems

Eine vollständig realisierte projektive Ebene weist eine unglaubliche Ausgewogenheit auf:
- Jedes Symbol erscheint gleich oft.
- Jede Karte verhält sich identisch.
- Das gesamte System ist symmetrisch und „fair”.
Diese Symmetrie verleiht Spot It! sein reibungsloses Gameplay, bei dem keine Karte leichter oder schwieriger zuzuordnen ist als andere.
7. Können Sie Ihr eigenes Spot It!-Kartenspiel entwerfen?
Ja! Solange Sie Folgendes beachten:
- Wählen Sie eine Primzahl n.
- Verwenden Sie n² + n + 1 als Gesamtzahl der Symbole und Karten.
- Setzen Sie n + 1 Symbole auf jede Karte.
- Konstruieren Sie mit modularer Arithmetik oder einem Projektivflächen-Generator.
Zum Beispiel:
| n | Symbole pro Karte | Gesamtzahl der Karten | Anmerkungen |
|---|---|---|---|
| 2 | 3 | 7 | Kleines Demo-Set |
| 3 | 4 | 13 | Kleine thematische Optionen |
| 5 | 6 | 31 | Beliebte benutzerdefinierte Größe |
| 7 | 8 | 57 | Klassische Spot It!-Größe |
Aus diesem Grund verwenden von Fans erstellte Print-and-Play-Versionen (PnP) oft Primzahlen.