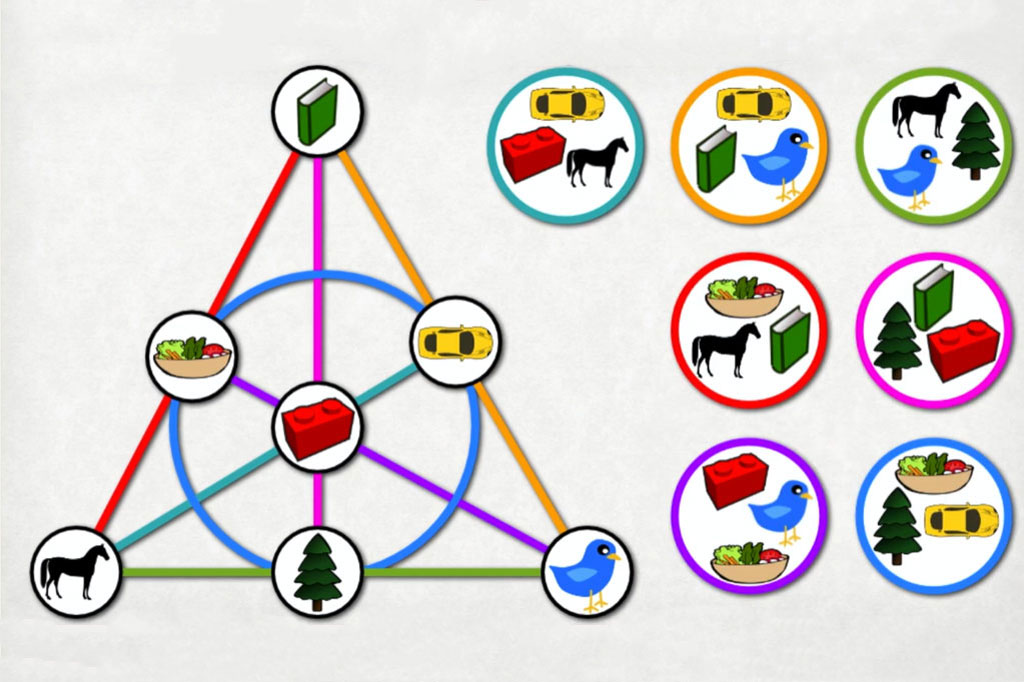
Si alguna vez has jugado a Spot It! (también conocido como Dobble), probablemente te hayas hecho la misma pregunta que millones de jugadores:
¿Cómo es posible que cada par de cartas comparta exactamente UN símbolo coincidente?
Parece magia… pero en realidad se trata de matemáticas, concretamente, de planos proyectivos finitos, combinatoria y aritmética modular.
Table of Contents
1. El concepto matemático fundamental: planos proyectivos finitos
Una baraja estándar de Spot It! se basa en la estructura de un plano proyectivo finito de orden n.
Un plano proyectivo de orden n tiene estas propiedades:
- Cada carta tiene (n + 1) símbolos.
- Hay (n² + n + 1) símbolos en total.
- Hay (n² + n + 1) cartas en total.
- Cualquier par de cartas comparte exactamente UN símbolo.
- Cualquier par de símbolos aparece junto en exactamente UNA carta.
Para Spot It!, el orden utilizado es:
- n = 7
Lo que da:
- Símbolos por carta: n + 1 = 8
- Cartas en la baraja: n² + n + 1 = 57
- Símbolos únicos: 57
Esto explica por qué las barajas de Spot It! suelen tener 55 cartas (se eliminan dos para que quepan en la caja).
2. Por qué solo funciona un símbolo coincidente
Matemáticamente, si cada par de cartas debe tener exactamente un símbolo en común (ni más ni menos), la estructura debe evitar:
- cero coincidencias (subsuperposición)
- múltiples coincidencias (superposición)
El diseño de un plano proyectivo garantiza esto:
- Cada símbolo aparece en n + 1 cartas.
- Cada carta tiene n + 1 símbolos.
- La distribución de los símbolos se equilibra mediante construcciones aritméticas modulares.
3. Cómo se generan realmente las cartas
Este es el método constructivo simplificado que se utiliza para crear una baraja cuando n es primo (como 7).
Paso A: Crear la carta «infinita»
Símbolos:
- ∞, a0, a1, a2, a3, a4, a5, a6 (8 símbolos en total)
Paso B: Crear n grupos de n cartas
Para cada fila r (0-6) y cada columna c (0-6), crear una carta:
- símbolo: a_r
- más los símbolos b_{(r×1+c)}, b_{(r×2+c)}, …, b_{(r×7+c)} (todos módulo 7)
Esto garantiza que las alineaciones de patrones siempre se superpongan una y solo una vez.
Paso C: Añadir las n + 1 cartas «inclinadas» finales
Estas garantizan que las relaciones diagonales coincidan según lo requiere el plano proyectivo.
Una vez montado, el mazo forma una estructura matemática perfecta en la que:
- Cada carta se cruza con todas las demás cartas en exactamente un símbolo.
4. Por qué son importantes los números primos
Esta construcción funciona perfectamente cuando n es un número primo (2, 3, 5, 7, 11, …) o una potencia prima.
Por eso Spot It! utiliza:
- n = 7 (un número primo)
- Cartas = 57 (máximo posible para este orden)
Si intentas construir tu propio juego con:
- n = 6
- n = 10
- n = 12
Descubrirás rápidamente que es imposible cumplir la regla de «una sola coincidencia», ya que los planos proyectivos no existen para la mayoría de los órdenes que no son potencias primarias.
5. Por qué el mazo tiene 55 cartas y no 57
En teoría, un plano proyectivo perfecto n = 7 da 57 cartas.
Pero las barajas de Spot It! suelen venir con:
- 55 cartas (estándar)
- 31 cartas (versión Junior)
- Recuentos temáticos personalizados
Los fabricantes recortan la baraja por:
- Consistencia del tamaño de la caja
- Coste de fabricación
- Juegos temáticos
- Opciones de diseño de expansión
Incluso con cartas eliminadas, la estructura de emparejamiento sigue pareciendo «mágica» para los jugadores.
6. La hermosa simetría del sistema

Un plano proyectivo completamente realizado tiene un equilibrio increíble:
- Cada símbolo aparece el mismo número de veces.
- Todas las cartas se comportan de forma idéntica.
- Todo el sistema es simétrico y «justo».
Esta simetría es la que da a Spot It! su fluidez de juego, en el que ninguna carta es más fácil o más difícil de emparejar que otras.
7. ¿Puedes diseñar tu propio mazo Spot It!
Sí, siempre que sigas estos pasos:
- Elige un número primo n.
- Utiliza n² + n + 1 como total de símbolos y cartas.
- Pon n + 1 símbolos en cada carta.
- Constrúyelo utilizando aritmética modular o un generador de planos proyectivos.
Por ejemplo:
| n | Símbolos por carta | Total de cartas | Notas |
|---|---|---|---|
| 2 | 3 | 7 | Pequeño juego de demostración |
| 3 | 4 | 13 | Pequeñas opciones temáticas |
| 5 | 6 | 31 | Tamaño personalizado popular |
| 7 | 8 | 57 | Tamaño clásico de Spot It! |
Por eso, las versiones Print-and-Play (PnP) creadas por fans suelen utilizar órdenes primos.