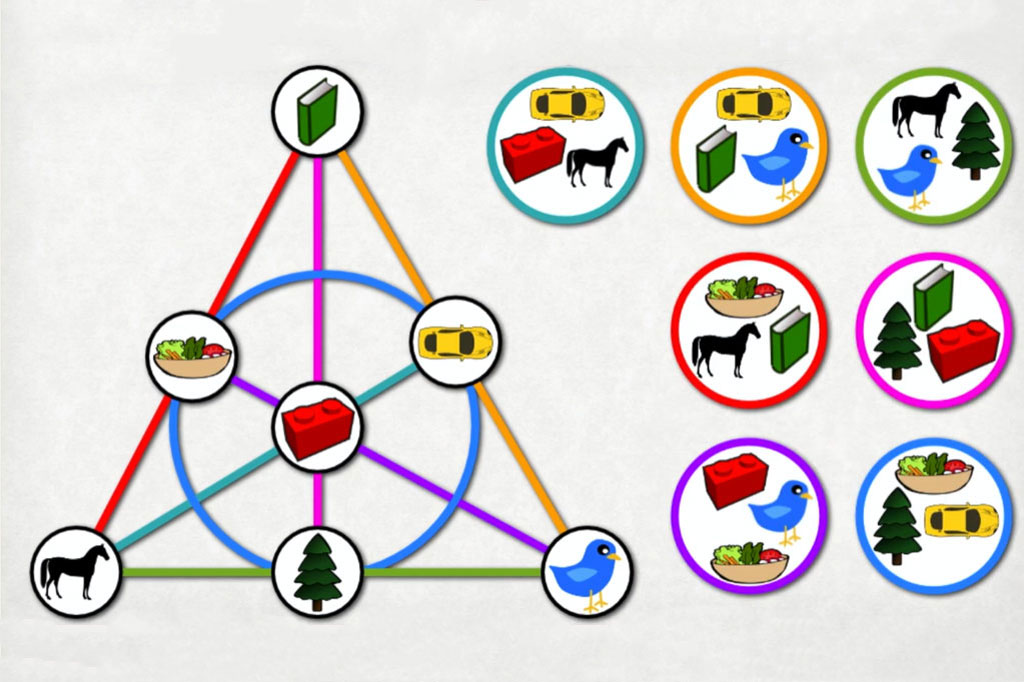
Om du någonsin haft spelat Spot It! (även känt som Dobble) har du förmodligen ställt samma fråga som miljontals andra spelare funderat över:
Hur i hela friden kan varje kortpar ha exakt ETT matchande symbol?
Det känns som magi… men det är faktiskt matematik, närmare bestämt finita projektiva plan, kombinatorik och modulär aritmetik.
Table of Contents
1. Det centrala matematiska begreppet: Finita projektiva plan
En standardkortlek i Spot It! baseras på strukturen hos ett finit projektivt plan av ordning n.
Ett projektivt plan av ordning n har följande egenskaper:
- Varje kort har (n + 1) symboler.
- Det finns totalt (n² + n + 1) symboler.
- Det finns totalt (n² + n + 1) kort.
- Två valfria kort har exakt ETT gemensamt symbol.
- Två valfria symboler förekommer tillsammans på exakt ETT kort.
För Spot It! används följande ordning:
- n = 7
Vilket ger:
- Symboler per kort: n + 1 = 8
- Kort i kortleken: n² + n + 1 = 57
- Unika symboler: 57
Detta förklarar varför Spot It!-kortlekar vanligtvis har 55 kort (två tas bort för att passa i förpackningen).
2. Varför endast ett matchande symbol fungerar
Matematiskt sett, om varje kortpar måste ha exakt ett symbol gemensamt (varken mer eller mindre), måste strukturen förhindra:
- noll matchningar (underlap)
- flera matchningar (overlap)
En projektiv plans design garanterar detta:
- Varje symbol förekommer på n + 1 kort.
- Varje kort har n + 1 symboler.
- Symbolfördelningen balanseras genom modulära aritmetiska konstruktioner.
3. Hur korten faktiskt genereras
Här är den förenklade konstruktiva metoden som används för att bygga en kortlek när n är ett primtal (som 7).
Steg A: Skapa det ”oändliga” kortet
Symboler:
- ∞, a0, a1, a2, a3, a4, a5, a6 (totalt 8 symboler)
Steg B: Skapa n grupper med n kort
För varje rad r (0–6) och varje kolumn c (0–6) skapar du ett kort:
- symbol: a_r
- plus symbolerna b_{(r×1+c)}, b_{(r×2+c)}, …, b_{(r×7+c)} (alla modulo 7)
Detta säkerställer att mönsterinriktningarna alltid överlappar varandra en gång och endast en gång.
Steg C: Lägg till de sista n + 1 ”lutningskorten”
Dessa säkerställer att diagonala relationer matchar enligt kraven för det projektiva planet.
När kortleken är sammansatt bildar den en perfekt matematisk struktur där:
- Varje kort skär varje annat kort vid exakt ett symbol.
4. Varför primtal är viktiga
Denna konstruktion fungerar smidigt när n är ett primtal (2, 3, 5, 7, 11, …) eller en primtalspotens.
Det är därför Spot It! använder:
- n = 7 (ett primtal)
- Kort = 57 (maximalt möjligt för denna ordning)
Om du försöker bygga din egen uppsättning med:
- n = 6
- n = 10
- n = 12
kommer du snabbt att upptäcka att det är omöjligt att uppfylla regeln om ”endast en matchning” eftersom projektiva plan inte existerar för de flesta ordningar som inte är primtalspotenser.
5. Varför kortleken har 55 kort, inte 57
I teorin ger ett perfekt n = 7 projektivt plan 57 kort.
Men Spot It!-kortlekar levereras vanligtvis med:
- 55 kort (standard)
- 31 kort (juniorversion)
- Anpassade tematiska antal
Tillverkarna anpassar kortleken för:
- Konsekvent boxstorlek
- Tillverkningskostnad
- Tematiska set
- Utvidgningsdesignval
Även med borttagna kort känns matchningsstrukturen fortfarande ”magisk” för spelarna.
6. Systemets vackra symmetri

Ett fullt realiserat projektivt plan har en otrolig balans:
- Varje symbol förekommer samma antal gånger.
- Varje kort beter sig identiskt.
- Hela systemet är symmetriskt och ”rättvist”.
Det är denna symmetri som ger Spot It! sitt smidiga spelupplägg, där inget kort är lättare eller svårare att matcha än andra.
7. Kan du designa ditt eget Spot It!-kortlek?
Ja! Så länge du följer:
- Välj ett primtal n.
- Använd n² + n + 1 som totalt antal symboler och kort.
- Lägg n + 1 symboler på varje kort.
- Konstruera med hjälp av modulär aritmetik eller en projektiv plan-generator.
Till exempel:
| n | Symboler per kort | Totalt antal kort | Anmärkningar |
|---|---|---|---|
| 2 | 3 | 7 | Litet demoset |
| 3 | 4 | 13 | Små tematiska alternativ |
| 5 | 6 | 31 | Populär anpassad storlek |
| 7 | 8 | 57 | Klassisk Spot It!-storlek |
Det är därför fan-gjorda Print-and-Play (PnP)-versioner ofta använder primtal.