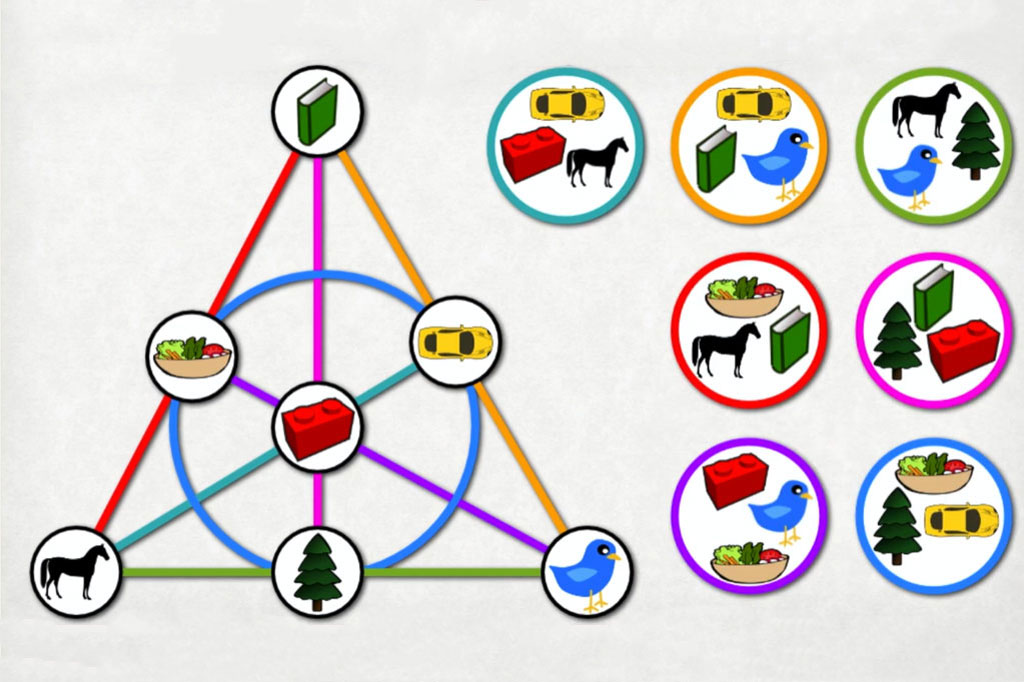
Si vous avez déjà joué à Spot It ! (également connu sous le nom de Dobble), vous vous êtes probablement posé la même question que des millions d’autres joueurs :
comment se fait-il que chaque paire de cartes partage exactement UN symbole commun ?
Cela semble magique… mais il s’agit en fait de mathématiques, plus précisément de plans projectifs finis, de combinatoire et d’arithmétique modulaire.
Table of Contents
1. Le concept mathématique fondamental : les plans projectifs finis
Un jeu de cartes Spot It! standard est basé sur la structure d’un plan projectif fini d’ordre n.
Un plan projectif d’ordre n possède les propriétés suivantes :
- Chaque carte comporte (n + 1) symboles.
- Il y a (n² + n + 1) symboles au total.
- Il y a (n² + n + 1) cartes au total.
- Deux cartes quelconques partagent exactement UN symbole.
- Deux symboles quelconques apparaissent ensemble sur exactement UNE carte.
Pour Spot It!, l’ordre utilisé est :
- n = 7
Ce qui donne :
- Symboles par carte : n + 1 = 8
- Cartes dans le jeu : n² + n + 1 = 57
- Symboles uniques : 57
Cela explique pourquoi les jeux Spot It! comptent généralement 55 cartes (deux sont retirées pour que le produit tienne dans la boîte).
2. Pourquoi un seul symbole correspondant fonctionne
Mathématiquement, si chaque paire de cartes doit avoir exactement un symbole en commun (ni plus, ni moins), la structure doit empêcher :
- les correspondances nulles (sous-recoupement)
- les correspondances multiples (recoupement)
La conception d’un plan projectif garantit cela :
- Chaque symbole apparaît sur n + 1 cartes.
- Chaque carte comporte n + 1 symboles.
- La distribution des symboles est équilibrée grâce à des constructions arithmétiques modulaires.
3. Comment les cartes sont-elles réellement générées ?
Voici la méthode constructive simplifiée utilisée pour construire un jeu lorsque n est un nombre premier (comme 7).
Étape A : Créer la carte « infinie »
Symboles :
- ∞, a0, a1, a2, a3, a4, a5, a6 (8 symboles au total)
Étape B : Créer n groupes de n cartes
Pour chaque ligne r (0-6) et chaque colonne c (0-6), créer une carte :
- symbole : a_r
- plus les symboles b_{(r×1+c)}, b_{(r×2+c)}, …, b_{(r×7+c)} (tous modulo 7)
Cela garantit que les alignements de motifs se chevauchent toujours une et une seule fois.
Étape C : Ajoutez les n + 1 cartes « pentes » finales
Celles-ci garantissent que les relations diagonales correspondent comme l’exige le plan projectif.
Une fois assemblé, le jeu forme une structure mathématique parfaite où :
- Chaque carte croise toutes les autres cartes à exactement un symbole.
4. Pourquoi les nombres premiers sont-ils importants ?
Cette construction fonctionne parfaitement lorsque n est un nombre premier (2, 3, 5, 7, 11, …) ou une puissance première.
C’est pourquoi Spot It! utilise :
- n = 7 (un nombre premier)
- Cartes = 57 (maximum possible pour cet ordre)
Si vous essayez de construire votre propre jeu avec :
- n = 6
- n = 10
- n = 12
Vous découvrirez rapidement qu’il est impossible de respecter la règle « une seule correspondance » car les plans projectifs n’existent pas pour la plupart des ordres qui ne sont pas des puissances de nombres premiers.
5. Pourquoi le jeu comporte 55 cartes et non 57
En théorie, un plan projectif parfait n = 7 donne 57 cartes.
Mais les jeux Spot It! sont généralement livrés avec :
- 55 cartes (standard)
- 31 cartes (version Junior)
- Nombre de cartes personnalisé selon le thème
Les fabricants réduisent le nombre de cartes pour :
- La cohérence de la taille de la boîte
- Le coût de fabrication
- Les jeux thématiques
- Les choix de conception des extensions
Même avec des cartes retirées, la structure de correspondance reste « magique » pour les joueurs.
6. La belle symétrie du système

Un plan projectif pleinement réalisé présente un équilibre incroyable :
- Chaque symbole apparaît le même nombre de fois.
- Chaque carte se comporte de manière identique.
- L’ensemble du système est symétrique et « équitable ».
C’est cette symétrie qui confère à Spot It! son gameplay fluide, où aucune carte n’est plus facile ou plus difficile à associer que les autres.
7. Pouvez-vous concevoir votre propre jeu Spot It! ?
Oui ! À condition de respecter les règles suivantes :
- Choisissez un nombre premier n.
- Utilisez n² + n + 1 comme nombre total de symboles et de cartes.
- Placez n + 1 symboles sur chaque carte.
- Construisez à l’aide de l’arithmétique modulaire ou d’un générateur de plan projectif.
Par exemple :
| n | Symboles par carte | Nombre total de cartes | Remarques |
|---|---|---|---|
| 2 | 3 | 7 | Petit jeu de démonstration |
| 3 | 4 | 13 | Petites options thématiques |
| 5 | 6 | 31 | Taille personnalisée populaire |
| 7 | 8 | 57 | Taille classique de Spot It! |
C’est pourquoi les versions Print-and-Play (PnP) créées par les fans utilisent souvent des ordres premiers.