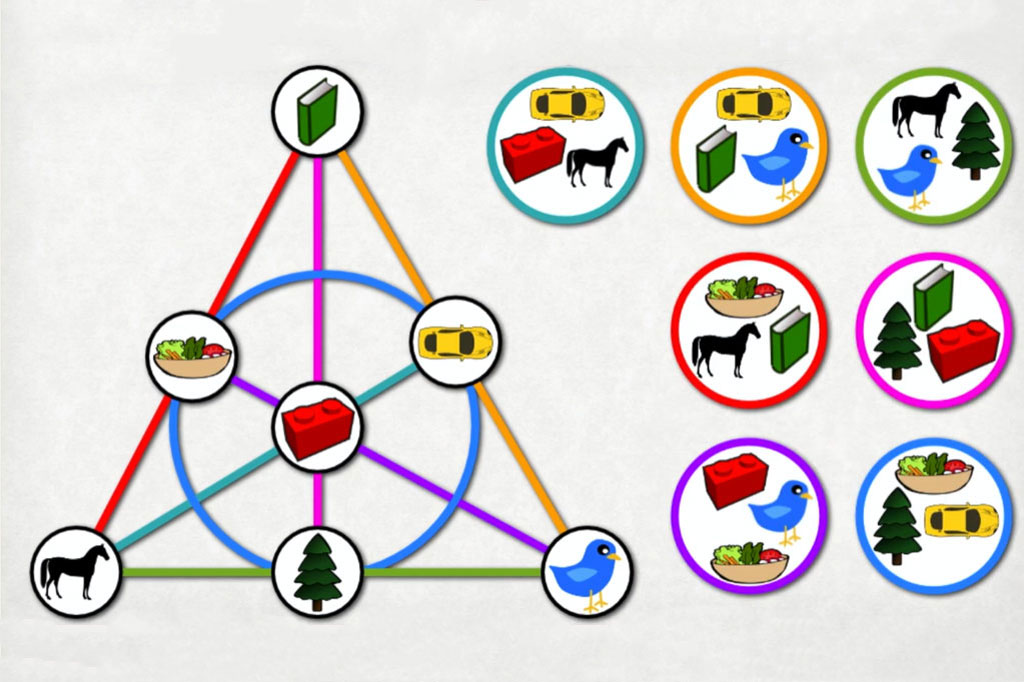
If you’ve ever played Spot It! (also known as Dobble), you’ve probably asked the same question millions of players have pondered:
How on earth does every pair of cards share exactly ONE matching symbol?
It feels like magic… but it’s actually mathematics, specifically, finite projective planes, combinatorics, and modular arithmetic.
Table of Contents
1. The Core Mathematical Concept: Finite Projective Planes
A standard Spot It! deck is based on the structure of a finite projective plane of order n.
A projective plane of order n has these properties:
- Each card has (n + 1) symbols.
- There are (n² + n + 1) total symbols.
- There are (n² + n + 1) total cards.
- Any two cards share exactly ONE symbol.
- Any two symbols appear together on exactly ONE card.
For Spot It!, the order used is:
- n = 7
Which gives:
- Symbols per card: n + 1 = 8
- Cards in deck: n² + n + 1 = 57
- Unique symbols: 57
This explains why Spot It! decks usually have 55 cards (two are removed to fit the boxed product).
2. Why Only One Matching Symbol Works
Mathematically, if each pair of cards must have exactly one symbol in common (no more, no less), the structure must prevent:
- zero matches (underlap)
- multiple matches (overlap)
A projective plane’s design guarantees this:
- Every symbol appears on n + 1 cards.
- Every card has n + 1 symbols.
- Symbol distribution is balanced through modular arithmetic constructions.
3. How the Cards Are Actually Generated
Here’s the simplified constructive method used for building a deck when n is prime (like 7).
Step A: Create the “infinite” card
Symbols:
- ∞, a0, a1, a2, a3, a4, a5, a6 (8 symbols total)
Step B: Create n groups of n cards
For each row r (0–6) and each column c (0–6), make a card:
- symbol: a_r
- plus the symbols b_{(r×1+c)}, b_{(r×2+c)}, …, b_{(r×7+c)} (all modulo 7)
This ensures that pattern alignments always overlap once and only once.
Step C: Add the final n + 1 “slope” cards
These ensure that diagonal relationships match as required by the projective plane.
When assembled, the deck forms a perfect mathematical structure where:
- Every card intersects every other card at exactly one symbol.
4. Why Prime Numbers Matter
This construction works cleanly when n is a prime number (2, 3, 5, 7, 11, …) or a prime power.
That’s why Spot It! uses:
- n = 7 (a prime)
- Cards = 57 (max possible for this order)
If you try to build your own set with:
- n = 6
- n = 10
- n = 12
You’ll quickly discover it’s impossible to satisfy the “one match only” rule because projective planes do not exist for most non-prime-power orders.
5. Why the Deck Has 55 Cards, Not 57
In theory, a perfect n = 7 projective plane gives 57 cards.
But Spot It! decks commonly ship with:
- 55 cards (standard)
- 31 cards (Junior version)
- Custom thematic counts
Manufacturers trim the deck for:
- Box size consistency
- Manufacturing cost
- Thematic sets
- Expansion design choices
Even with removed cards, the matching structure still feels “magical” to players.
6. The Beautiful Symmetry of the System

A fully realized projective plane has incredible balance:
- Every symbol appears the same number of times.
- Every card behaves identically.
- The entire system is symmetrical and “fair.”
This symmetry is what gives Spot It! its smooth gameplay, where no card is easier or harder to match than others.
7. Can You Design Your Own Spot It! Deck?
Yes! As long as you follow:
- Choose a prime number n.
- Use n² + n + 1 as your total symbols and cards.
- Put n + 1 symbols on each card.
- Construct using modular arithmetic or a projective plane generator.
For example:
| n | Symbols per card | Total cards | Notes |
|---|---|---|---|
| 2 | 3 | 7 | Tiny demo set |
| 3 | 4 | 13 | Small thematic options |
| 5 | 6 | 31 | Popular custom size |
| 7 | 8 | 57 | Classic Spot It! size |
This is why fan-made Print-and-Play (PnP) versions often use prime orders.